遷移状態を求めるのは難しい！！

構造最適化計算ではエネルギーが極小になる安定化構造を探索するのに対し、遷移状態計算では、エネルギーが極大値となる構造を求めます。ここでの極大とは、「ある方向で見れば極大値だが別の方向で見れば極小値」となる鞍点(saddle point/あんてん)を指します。
※有機化学の教科書なでよくみる遷移状態を表した2次元のエネルギーダイアグラム図は、N個の原子からなる分子の３N-６次元(直線分子では3N-5次元)のポテンシャル超曲面の一部を目的の反応について切り出したものです。実際の遷移状態が単にエネルギーの極大を求めているわけではないことに注意が必要です。

「ある方向で見れば極大値だが別の方向で見れば極小値」という概念はすこし理解しづらいかもしれません。そこで、「ある目的の反応についてはエネルギー極大(遷移状態)だが、別の反応については安定構造」と言い換えると、すこし分かりやすくなるかもしれません。遷移状態でも、反応と関係ない結合まで不安定であれば目的の化合物へ到達できないのはイメージとして理解できると思います。
つまり、反応とは関係ない結合については、遷移状態でも安定な平衡構造である必要があるのです。安定化構造の探索は全ての自由度に対してエネルギーの極小化を行えばよいのですが、遷移状態の探索は鞍点という特殊な構造のため、その探索は格段に難しくなります。構造最適化計算と異なり、時間をかければ必ず解が求まるわけではないので初心者にとって最初のハードルと言われる所以です。
 

なにより初期構造が重要！！

遷移状態を計算するには、遷移状態に近い初期構造を用意する必要があります。先程説明したような理由から、構造最適化計算で用意する初期構造よりも、求められる初期構造の正確性はさらに高くなります。あまりに異なった初期構造を利用すると、目的と異なった遷移構造が出力されたり、計算自体が収束せずに結果が全く得られなかったりします。

例えばGAMESSでは、$CONTRLグループでRUNTYP=SADPOINTを指定することで遷移状態の計算ができます。しかし、ここで利用する初期構造は真の遷移状態にかなり近くないと計算が上手くいきません。そこで、この計算を行う前にできるだけ遷移状態に近い構造を求めておくことが重要になります。

残念なことに全ての系に適した万能な遷移状態の探索方法はありません。対象とする系に応じてその都度、目的に合った探索方法を選ぶことが重要です。

遷移状態の探索方法

それでは早速、代表的な遷移状態の探索方法についてみていきましょう。

1) 置換基法
まず、初心者におすすめしたいのが置換基法です。この方法は、これまで紹介したデータベースなどから遷移状態構造をダウンロードし利用する方法です。求めたい系と似たような遷移状態がみつかれば、あとは置換基を目的の系に変更して再度計算すれば遷移状態が求まります。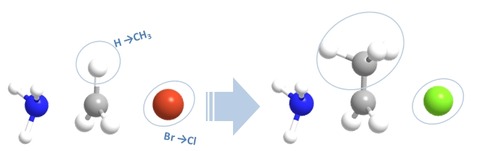

初心者にとっては、難しい操作を極力なくした最も簡便な方法と言えます。遷移状態において、置換基が直接反応に関与しない場合はうまくいくことが期待できます。デメリットは当然、データベースに存在しない遷移状態ではこの方法は使用できないことです。あとは、最初に使用した遷移状態に比べて、加えた置換基が反応部位で非常に込み合ってしまう場合や(立体障害が大きい)、置換基の自由度が高い場合などは、別途導入した置換基以外を固定して構造最適化するなど少し工夫しないと計算がうまく収束しない場合があることなどです。
まずは、この一番簡便な方法をマスターして遷移状態探索方法や計算方法の概略をつかむことをおすすめします。
 

2) SADDLE法
SADDLE法は、反応物と生成物の構造を入力するだけで、候補となる遷移状態構造を計算してくれます。残念ながら、この方法はGAMESSでは直接利用できないのでそのほかの計算ソフトを利用する必要があります。MOPACを利用すれば、比較的簡単にこの計算ができます。MOPAC6(又はMOPAC7)であればパブリックドメインになっているので、学生以外でも無償で利用できます(アカデミックであれば最新版のMOPACが利用できます)。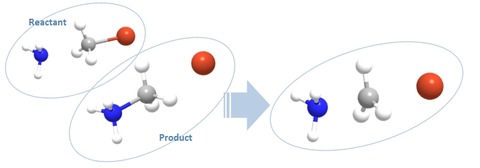

具体的には、反応物と生成物の座標を入力し、3N-6次元のポテンシャル超曲面における両極小点を結ぶ方向を基本的な反応座標の方向と考え、両構造からその直線上の極大点を探索していき遷移状態近傍の候補となる構造を探索します。この方法は反応自体があまり入り組んでない場合には非常に有効な方法です。ただし注意が必要なのは、反応物と生成物の各結合情報が一致していなければならないことです。例えば、反応前後で各原子に割り当てられる番号が異なっていれば計算が実行できないので、分子モデリングソフトで初期構造を作る際に少しだけ工夫が必要です。MOPACによるSADDLE計算の方法はこちらの記事を参照してみてください。
 

3) ミニマムエネルギーパス法 (Minimum Energy Path)
MEP法は、反応部位の結合距離や角度などを一方向に変化させながら、繰返し計算をおこない遷移状態を探索する方法です。入力ファイルの作成が少々煩雑になり、初心者には面倒に感じるかもしれません。置換基法やSADDLE法でうまくいかない場合に試してみましょう。

具体的には、求めたい遷移状態の反応を特徴づけるような内部座標を反応座標として選び、何点かの反応座標値を指定します。次に、各点での反応座標以外の自由度に関しては構造最適化を行ったエネルギー計算を実行します。そこで得られたエネルギープロファイルの極大点を、遷移状態近傍の構造であると仮定し、遷移状態の初期構造として利用します。
この手法は、真の反応座標が、反応座標として取り上げている内部座標に局在している場合にはうまくいくことが期待できます。デメリットは、入力ファイルの作成が面倒なのと、反応座標値毎に繰返し計算を行うので相応のCPU時間を要することです。GAMESSでもこの方法は実行できますが、入力ファイルの作成などMOPACで慣れてからGAMESSに進んだほうが、理解が深まると思います。MOPACでの実行方法はこちらの記事を参照してください。

4) エネルギー等高線図法
この方法は、MEP法と異なり結合距離や角度を二方向に変化させながら、繰返し計算をおこない遷移状態を探索する方法です。遷移状態付近で構造が急激に変化するなど、MEP法では上手く計算ができない場合に用いることが多いです。
例えば、反応に関係する2つのパラメーター(結合距離や角度)を固定した場合、他のパラメーターを最適化していきます。その際、固定した2つのパラメーターを順次変化させることで等高線図が得られます。後は、等高線の形状から遷移状態近傍の構造を抜き出し、遷移状態の初期構造として利用します。デメリットは、なんといっても等高線図を作成するのが面倒な点です。遷移状態計算の初期構造を探索する方法としては良い方法ですが、先の3つの方法でどうしても難しい場合の最終手段として実行する方が無難でしょう。
 

5) その他の新しい方法
上記のような従来の方法以外にも、新しい遷移状態の探索方法が開発されています。ここで紹介する方法は、計算コストが非常に高かかったり、有償であったりとこのブログの趣旨と少し離れてしますので簡単に紹介だけします。
 

5-1) GRRM法 (Global Reaction Route Mapping)
GRRMは「化学反応経路全自動探索プログラム」です。GAMESSとも組み合わせて使うことができます。この方法は、与えられた構造から、遷移状態がある方向へ分子を徐々に変形させながら、考えうるすべての反応経路を全自動で探索する方法です。すべての反応経路を計算するため、求めたい反応経路はかならずその中に見つかる反面、考えうる経路をすべて求めようとしてしまうため多大なCPU時間を要します。
アカデミックは条件を満たせば、普及用モニター版を無償で利用できます(非アカデミックは研究支援が必要)。興味がある方は、HPを覗いてみてください。　
 

5-2) NEB法 (Nudged Elastic Band)
NEB法が使える計算パッケージはいくつかあります。最近では、HPCシステムズより発売されたReaction Plusが有名ではないでしょうか。その他には、NWChemやOpenMX、VTSTなどでも利用できます(GAMESS(US)でのNEB法の実行方法はこちら)。
NEB法で指定するのは反応前後の構造だけです。具体的には、想定している反応の２つの構造(反応物と生成物)の数値的な平均構造を作りエネルギー表面上に等間隔に配置します。次に生成した各点を結びます。この各点を結んだものをElastic Bandと呼び、反応経路であるポテンシャルエネルギー曲面へ向かってElastic Bandを最適化していきます。仮の反応経路(Elastic Band)をまず求めて、そこから真の反応経路に向かって最適化していくといったイメージですね。
Reaction Plusは有償ですが、体験版も用意されているので興味がある方は、HPを覗いてみてください。

おわりに

今回は、構造最適化に比べ遷移状態を求めることの難しさや、そのために初期構造が重要であること、遷移状態の初期構造の求め方として代表的な方法をいくつか紹介しました。遷移状態の探索で「これが正解」という方法は存在しません。ここで上げた幾つかの方法も、実際に計算するユーザーによって更に細かいノウハウがあったりします。計算する系によって、これらのノウハウ部分は異なるのでなかなか表には出ませんし、各研究機関などで秘匿される傾向にあります。まずは、代表的な方法をマスターして自分の計算したい系ではどの方法が最適かを見極めることが重要です。次第に、経験を通して独自のノウハウが積み上がっていくはずです。
ここで紹介した方法については、実際に手を動かしながら「体験」することで習得していきましょう。まずは、簡単な系から徐々にステップアップしていくことが一番の近道です。

※) 当ブログの連載が書籍になりました！！興味がある方は、お手に取っていただければ幸いです！！
(Amazon購入ページ)（書籍の紹介記事）


【関連記事】
遷移状態を求めよう！！その②～実践編～
遷移状態を「SADDLE法」で探索しよう
遷移状態を「MEP法」で探索しよう